Wykres to jedno z podstawowych narzędzi do odnajdywania wzorców w danych i osobiście wykonuję ich setki. Zdecydowana większość z nich jest tylko dla mnie, ale część zostaje gdzieś opublikowana, na przykład w formie prezentacji. Takie wykresy mają być wiarygodnym/uczciwym podsumowaniem wykrytych przeze mnie zależności i pomóc czytelnikowi w zauważeniu tego, co sam zauważyłem.
Oczywiście taki wykres trzeba umiejętnie wykonać. Najogólniej można powiedzieć, że powinien przedstawiać takie różnice/zależności, jakie są w rzeczywistości. Jeśli są niewielkie, takie właśnie wrażenie powinien mieć odbiorca, patrząc na wykres.
Zdarza się, że tak nie jest. Możemy wyróżnić tu dwa przypadki:
- Autor wykresu nie ma odpowiednich umiejętności.
- Autor wykorzystuje swoje umiejętności, żeby manipulować odbiorcą, na przykład „podkręcając” pewne różnice, które tak naprawdę są niewielkie.
W obu przypadkach wykresy wprowadzają w błąd, więc są szkodliwe, choć groźniejsza jest oczywiście druga sytuacja. Można powiedzieć, że jeśli ktoś się nie zna, będzie popełniał błędy „losowo”, przez co czasem zawyży różnice, czasem zaniży. W drugim przypadku działanie jest kierunkowe.
Motywacją plebiscytu (który jest kontynuacją plebiscytów organizowanych wcześniej przez Przemysława Biecka) jest uodpornienie nas na takie manipulacje, poprzez pokazanie konkretnych przykładów. Być może dzięki temu „sprzedawcy nieprawd” będą mieli trudniejsze zadanie.
Zasady plebiscytu
Z nadesłanych przez Was wykresów wybrałem 16 kandydatów. Wszystkie zostały gdzieś opublikowane, ale o ile było to możliwe, usunąłem informację o źródle. Wynika to z tego, że tylko niektóre z nich można zakwalifikować jako celowo wprowadzające w błąd. Większość jest po prostu źle wykonana, co najpewniej wynika z niewiedzy – a celem plebiscytu jest krytykowanie wykresów, a nie ich autorów.
Na wykresy można było głosować w czterech ankietach (półfinałach) na Linkedin. W każdym wystąpiły cztery wykresy i wybrano po jednym. Następnie spotkały się w ostatniej ankiecie, wielkim finale. Zwyciężył wykres nr 4 („porody”), drugie miejsce zajął nr 14 („czas antenowy w TVP”), trzecie nr 6 („poparcie dla Konfederacji”).
W sumie w pięciu ankietach oddano prawie 1400 głosów. Walka między dwoma najgorszymi wykresami była zażarta i różnica między nimi wyniosła jedynie kilka głosów.
Poniżej przedstawienie wszystkich kandydatów. Prezentując każdego, starałem się wypunktować, co jest w nim złego oraz jak można to poprawić. Częściowo jest to subiektywne, bo mówimy tu o tym, jakie wrażenie powinien mieć odbiorca, patrząc na wykres – a to przecież zależy też od odbiorcy. W większości jednak są to „klasyczne” błędy, znane od lat.
Wykres 1
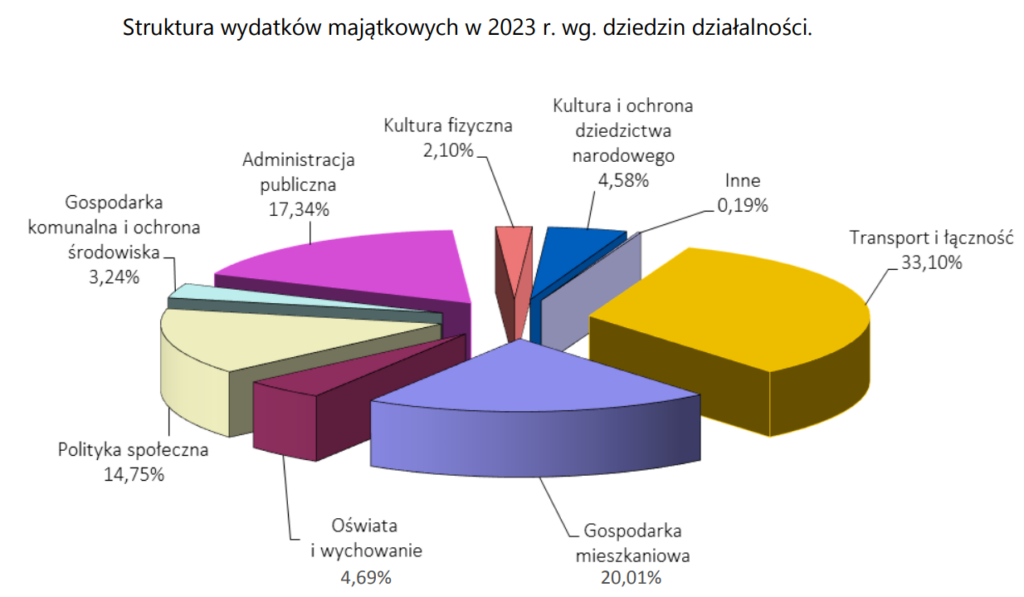
Zaczynamy od klasyki, czyli wykresu kołowego, na dodatek w swej najgorszej odsłonie, czyli 3D. Ciężko wybrać gorszy sposób prezentacji takich danych. Spójrzmy na przykład na kategorie „Gospodarka mieszkaniowa” i „Administracja publiczna”. Mimo że różnice nie są duże (20% vs. 17%), na wykresie ta pierwsza kategoria zajmuje znacznie więcej miejsca (porównajmy z wykresem słupkowym poniżej).
Warto dodać, że istnieją przypadki, w których wykres kołowy się sprawdzi (choć nigdy 3D). Ale to nie jest ten przypadek.
Jak to zrobić lepiej? Prawie zawsze dobry będzie wykres słupkowy, jak ten niżej.
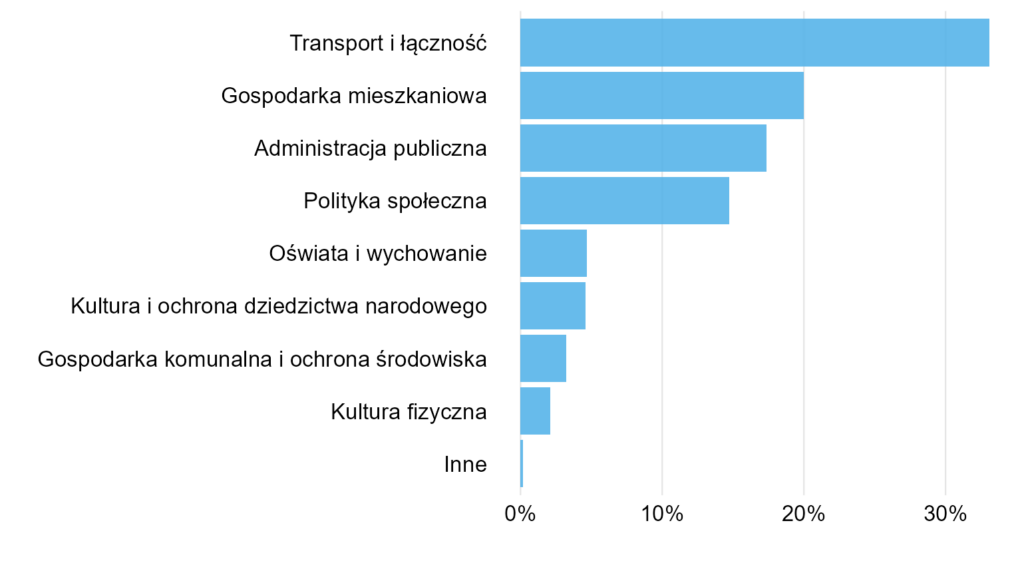
Jeśli chcemy, możemy dorzucić etykiety z wartościami liczbowymi, choć wtedy oś X staje się zbędna. Nie warto jednak podawać ich aż tak dokładnie (dwa miejsca po przecinku), jak to miało miejsce w oryginalnym wykresie.
Wykres 2
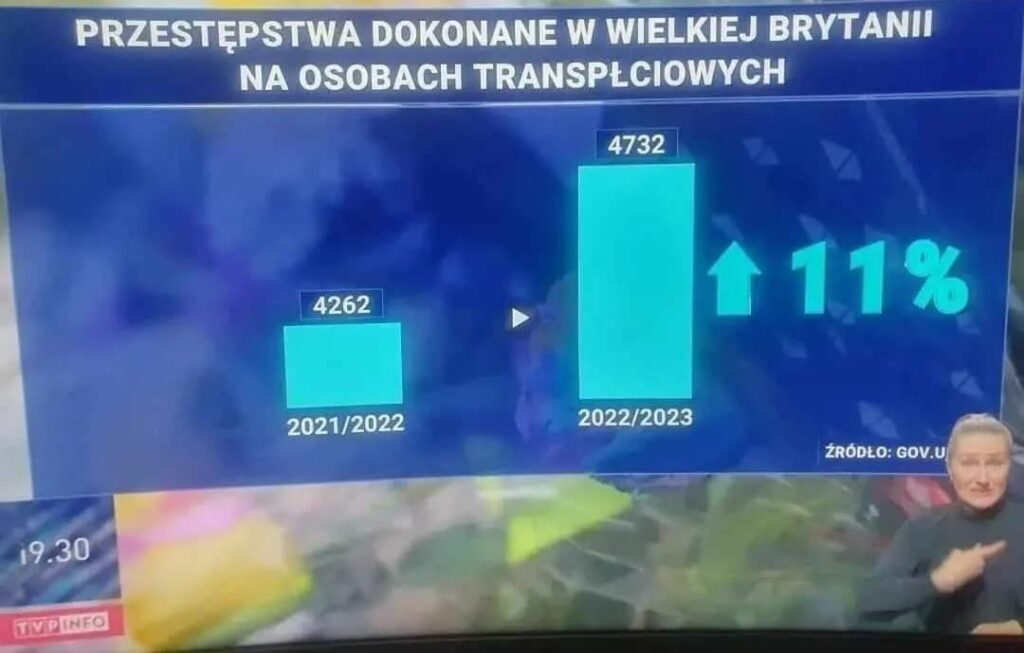
Znów klasyczny przykład, w którym oś Y zaczyna się w przypadkowym miejscu – czy raczej takim, by różnica wydawała się znacznie większa, niż w rzeczywistości. Oczywiście wzrost 11% można potraktować jako duży, ale już lepiej było pokazać jedynie tę wartość (wraz z liczbą przestępstw), rezygnując ze słupków.
Dla porównania, dołączam wersję tego wykresu, w którym oś Y zaczyna się w zerze.
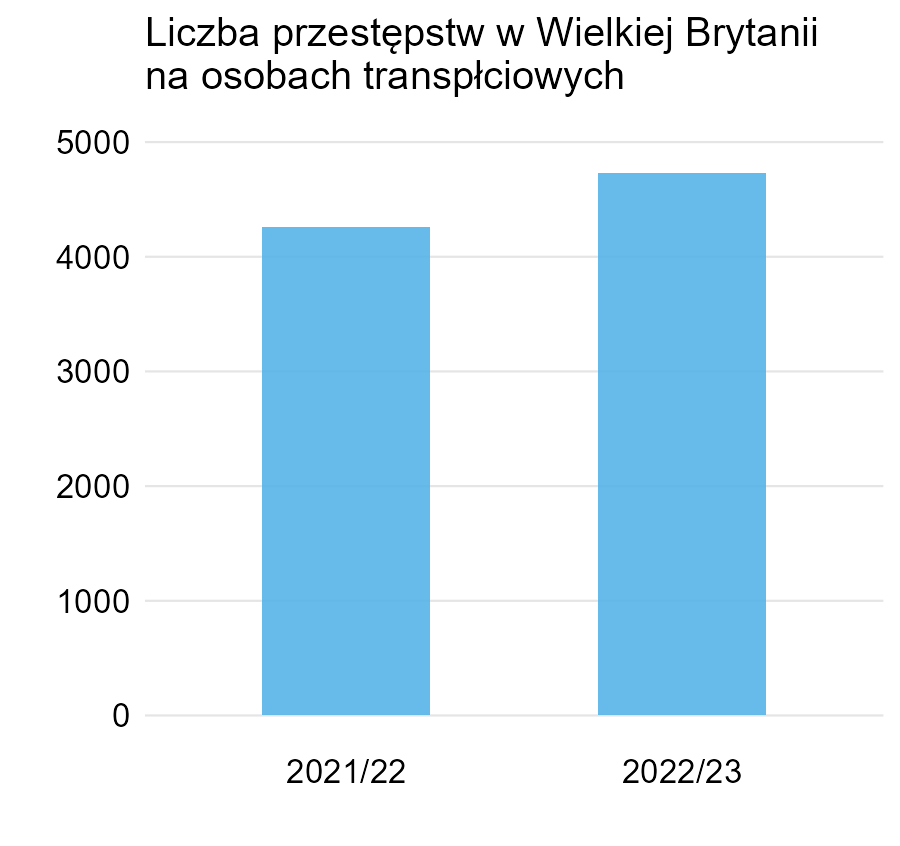
Warto jeszcze dodać, że ponieważ pokazano dane tylko z dwóch okresów, ocena wielkości różnicy między nimi jest utrudniona. Być może różnice na poziomie +/- 11% były częste we wcześniejszych latach (i nie mamy do czynienia z trendem, ale czasem były dodatnie, a czasem ujemne).
Wykres 3
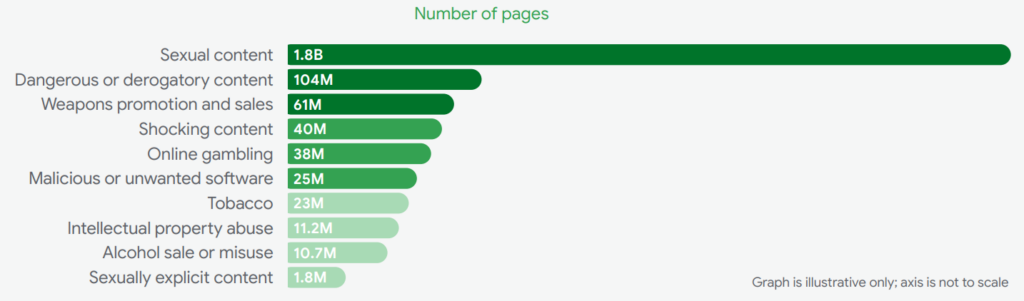
Głównym problemem jest tu długość słupków, która ma się nijak do liczb. Co prawda w rogu jest adnotacja, że wykres jest tylko w celach „ilustracyjnych” (to dobrze), ale takie ostrzeżenie w niewielkim stopniu wpływa na percepcję. Wykresy nie są do czytania, ale przede wszystkim do oglądania. Poza tym w dużej mierze bazują na tym, że wiemy, czego się spodziewać – czyli w tym przypadku, że długość słupka powinna być proporcjonalna do liczb.
Oprócz tego mamy tu niepotrzebny gradient. Dlaczego „Tobacco” (23M) jest znacznie jaśniejsze od „Malicious or unwanted software” (25M), skoro różnica w liczbach jest minimalna? Mylące może być też to, że wszystkie wartości są podane w milionach (M) poza pierwszą kategorią (B).
Jak to poprawić? Nie jest to oczywiste. Zacznijmy od wykresu słupkowego, w którym proporcje będą zachowane.
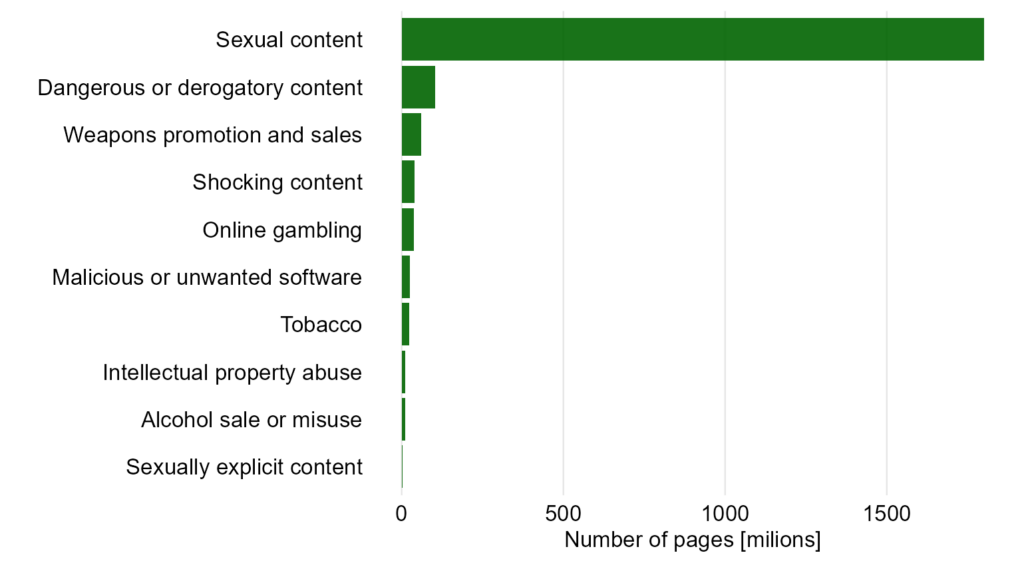
Poza pierwszą kategorią różnice wydają się minimalne – bo w porównaniu do niej rzeczywiście tak jest. Co jednak, gdy te pozostałe różnice też są ważne i chcemy je lepiej pokazać? Możemy zastanowić się nad skalą logarytmiczną, jak niżej. Natomiast ma to sens wtedy, kiedy liczą się tylko rzędy wielkości (10, 100, 1000). Oprócz tego czytelnik może nie być zaznajomiony z tą skalą i ostatecznie odniesie jeszcze gorsze wrażenie co do wielkości różnic, niż w przypadku tego oryginalnego wykresu, który krytykujemy.
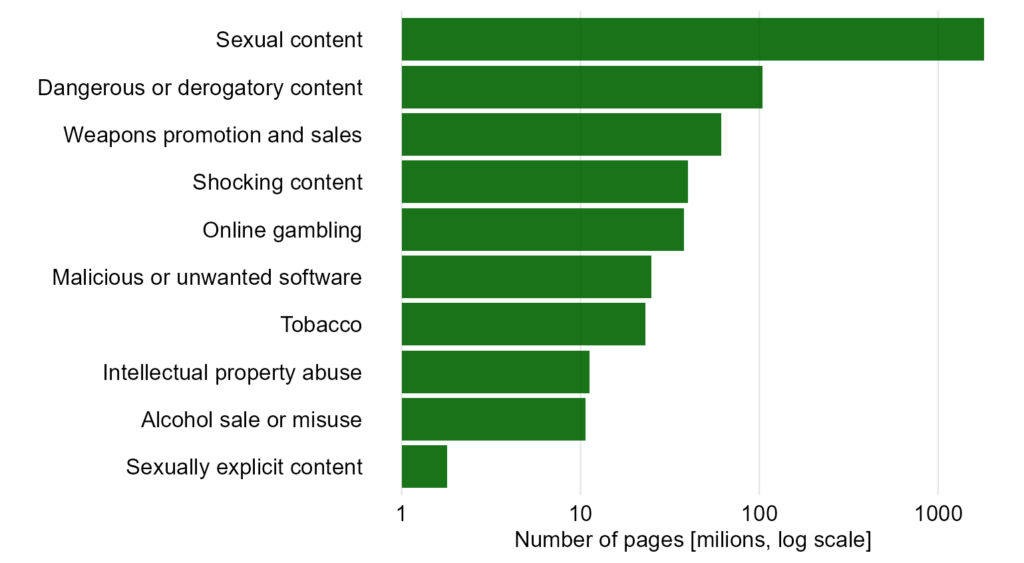
Dlatego w tym przypadku najlepszym pomysłem mogą być po prostu dwa wykresy. Na pierwszym pokazujemy pierwszą kategorię w porównaniu z resztą, a na drugim wszystkie kategorie poza pierwszą.
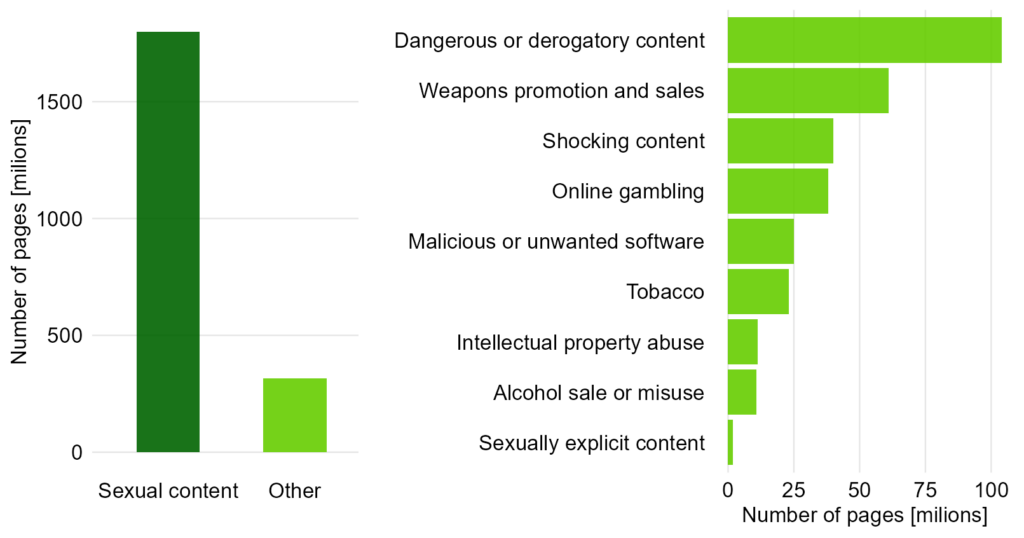
Warto też dodatkowo zaznaczyć, że kategorie po prawej stronie tworzą „Other”, na przykład przy pomocy strzałki (tutaj pokazałem to tylko kolorem). Można też ostrzec czytelnika, że skale na osiach są zupełnie inne, choć moim zdaniem tak, jak teraz, jest wystarczające.
Wykres 4
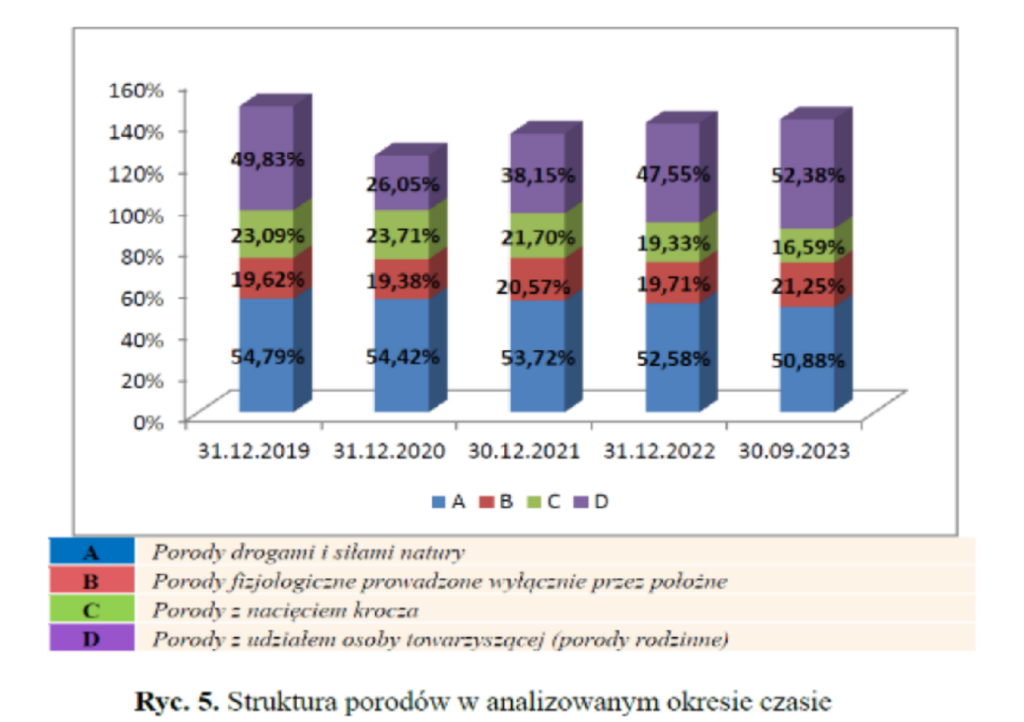
Mamy tutaj przykład tak zwanego pytania wielokrotnego wyboru, stąd całkowita długość słupka jest powyżej 100% i nie ma żadnego sensu. Nie da się porównać (wizualnie) żadnej kategorii poza „A”, choć nawet to jest utrudnione przez użycie efektu 3D.
Jak poprawić ten wykres? Można było przedstawić słupki dla każdej kategorii obok siebie i już byłoby znacznie lepiej, ale moim zdaniem jeszcze lepiej sprawdzi się tutaj wykres liniowy.
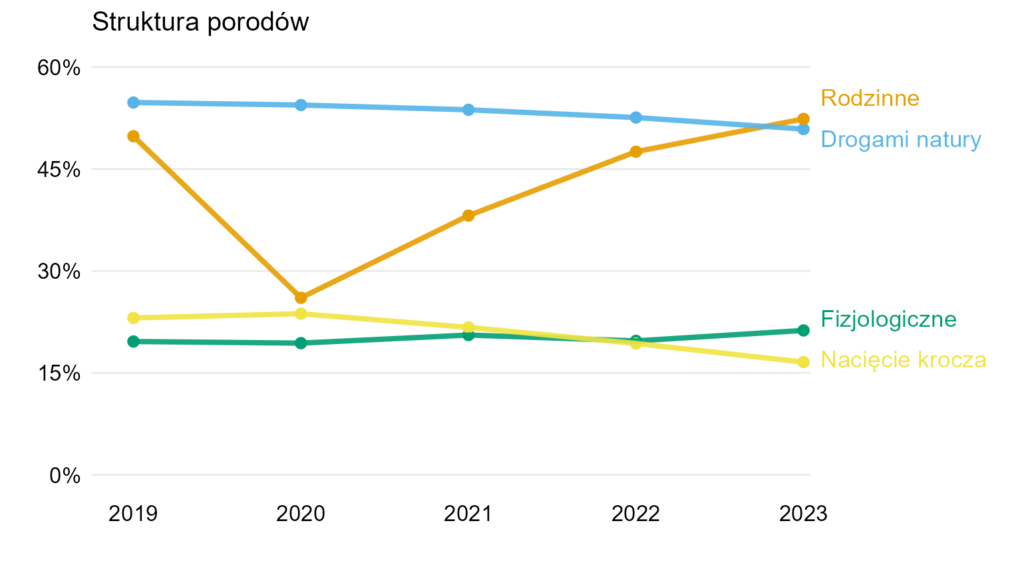
Teraz bardzo dobrze widać, jak spadła liczba porodów rodzinnych (COVID), ale w 2023 roku wróciła do stanu z 2019 (a nawet jest ich trochę więcej).
Warto odnotować, że dane dla ostatniego roku są 30 września, a nie z końca grudnia. Stąd jeśli widoczny trend się utrzyma, na przykład porodów rodzinnych za cały rok 2023 może być jeszcze trochę więcej. Moim zdaniem najlepiej umieścić tę informację w opisie wykresu.
Wykres 5
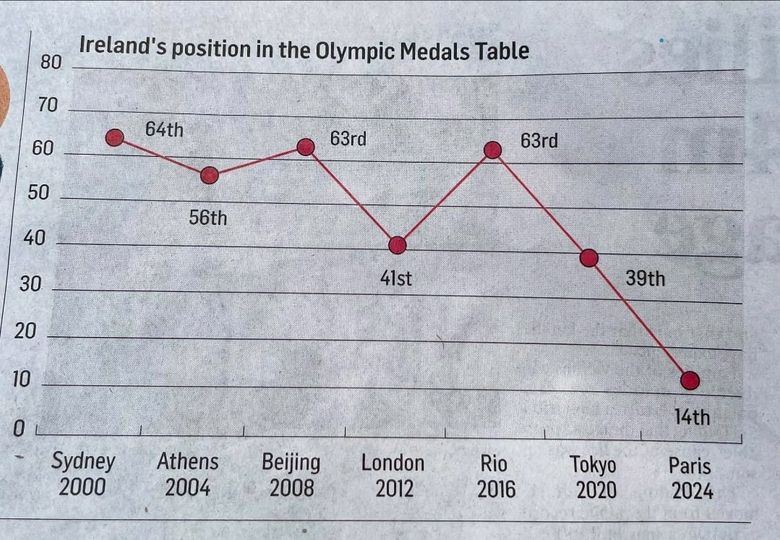
Na pierwszy rzut oka Irlandia na ostatnich igrzyskach olimpijskich poradziła sobie najgorzej (wykres biegnie „w dół”). Oczywiście gdy skupimy się na wykresie, to będzie jasne, że jest odwrotnie – ale ten „pierwszy rzut oka” w przypadku wykresów jest ważny.
Jest tu też problem z zerem (nie ma takiej pozycji). Oprócz tego dane na wykresie są zwyczajnie nieprawdzie: w 2004 Irlandia nie zdobyła żadnego medalu i nie zajęła 56. miejsca. Co prawda przez pewien czas miała złoto w skokach przez przeszkody (jeździectwo), ale został jej odebrany za doping. Podaję to jako ostatnią wadę, bo skupiamy się na problemach z samymi wykresami, ale patrząc całościowo, poprawność danych to znacznie ważniejsza kwestia.
Jak to poprawić? Bardzo dobre propozycje można znaleźć tutaj i raczej nie mam nic więcej do dodatnia.
Wykres 6
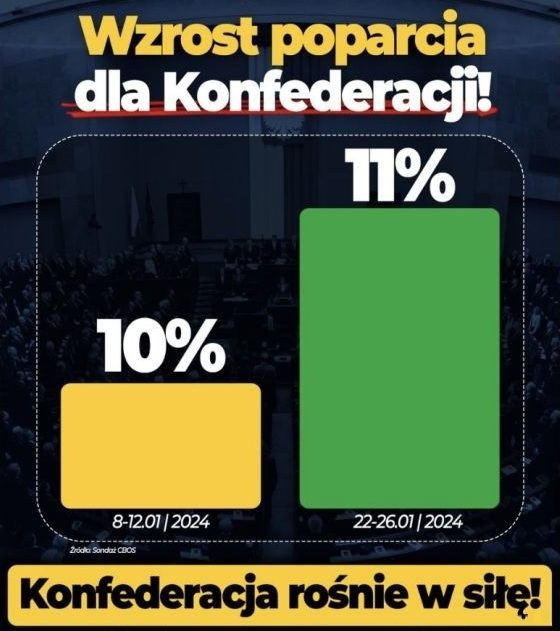
Mimo minimalnej różnicy drugi słupek jest ponad dwukrotnie wyższy. Oprócz tego kolor zmienia się z żółtego na zielony (to nie jest przypadek). Ogólnie znów mamy tu problem z osią Y, która nie zaczyna się w zerze, natomiast warto jeszcze zauważyć, że jest to sondaż wyborczy, więc podane wartości to nie jest poparcie, ale jej szacunek. Co więcej, dla 1000 obserwacji (a to jest typowa próba dla sondaży) błąd standardowy dla szacowania proporcji 10% wynosi około 1% (ten błąd zależy od rzeczywistej proporcji!), czyli właśnie tyle, ile wynosi różnica między tymi sondażami. Stąd można się zastanawiać, na ile tytuł jest poprawny.
Obrona tego wykresu to machnięcie ręką, że to przecież „plakat wyborczy”. Oczywiście – ale fakt, że coś z założenia ma być manipulacją/propagandą nie sprawia, że przestaje takie być.
Poniżej te same dane, ale oś Y zaczyna się w zerze.
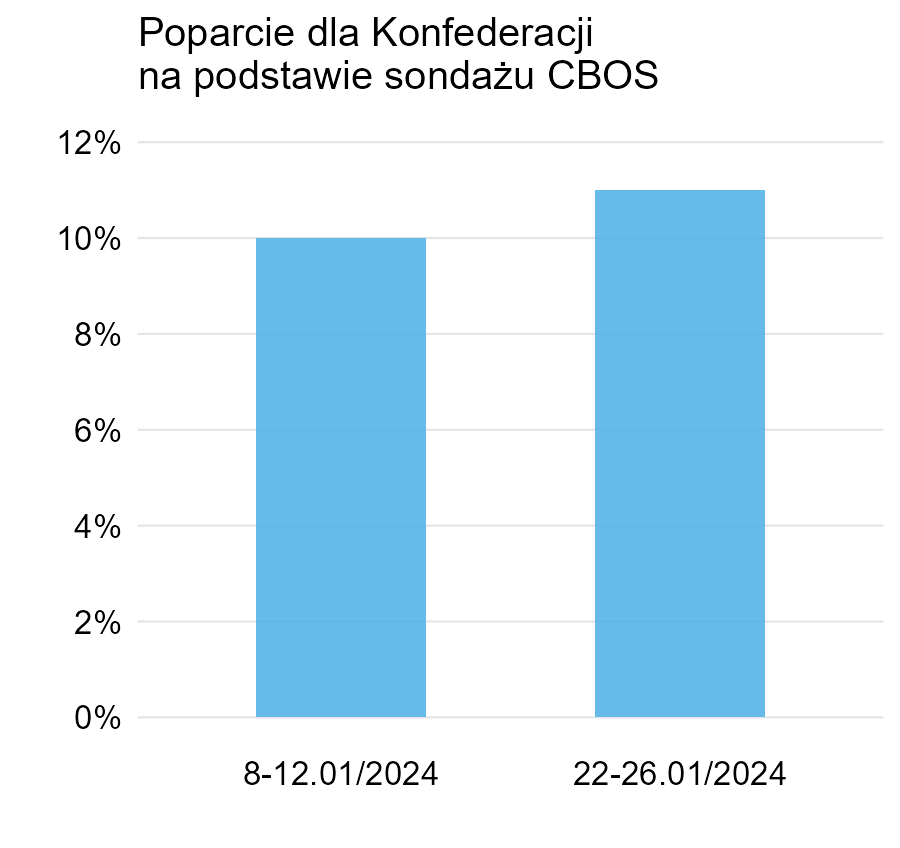
Wykres 7
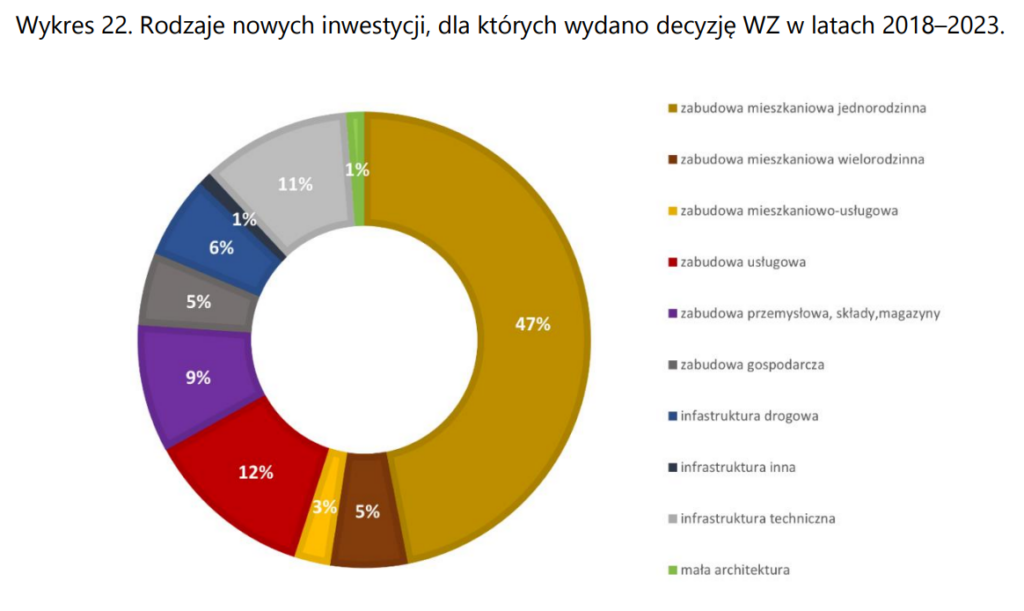
Jedyna zaletą tego wykresu kołowego jest to, że nie jest 3D. Ale można argumentować, że i tak jest gorszy od poprzedniego (wykres 1), bo wymaga od czytelnika, by dopasował kategorię z legendy do wartości na wykresie (poprzednio pojawiły się one obok odpowiednich „kawałków tortu”). Nie jest to proste, choć jak przyjrzymy się legendzie, kolejność etykiet odpowiada kolejności na wykresie. Która jednak nie wydaje się mieć dużego sensu i lepiej byłoby posortować kategorie od najczęstszej do najrzadszej.
Jak poprawić ten wykres? Nie ma sensu kombinować, znów wystarczy wykres słupkowy.
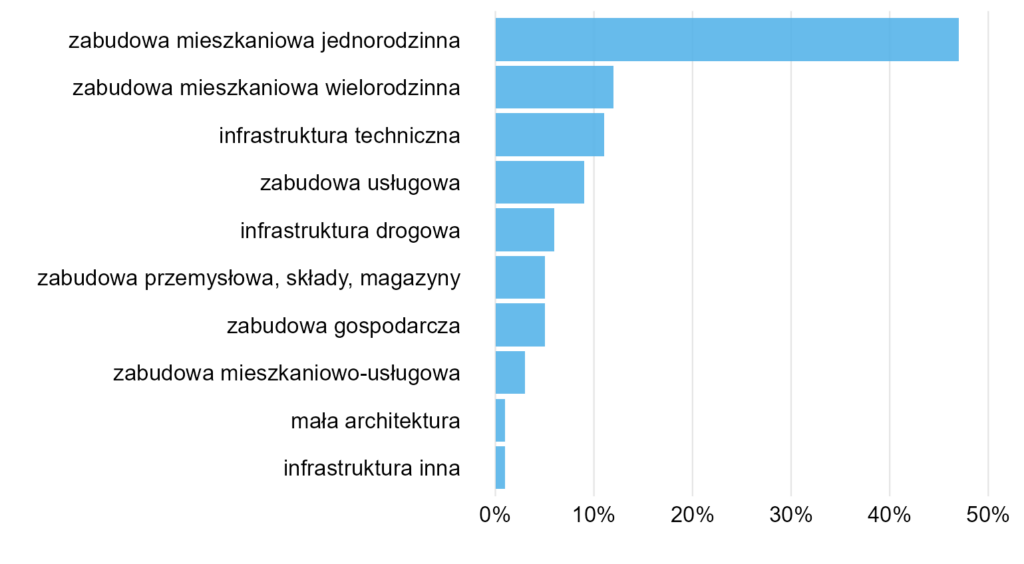
Dodajmy, że nie zawsze kolejność od najczęstszej kategorii do najrzadszej jest najlepsza. Czasem możemy mieć do czynienia z pewną „naturalną” kolejnością, która warto zachować.
Wykres 8
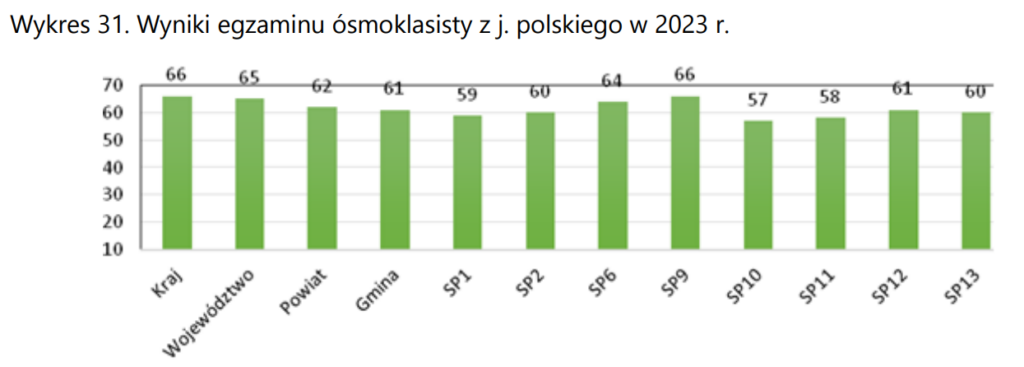
Ciekawy przykład, w który jest problem zarówno z początkiem osi Y, jak i z końcem. Oprócz tego nie jest jasne, czym są podane liczby (są to procenty). Z jakiegoś powodu ktoś wpadł na pomysł, żeby zacząć wykres od 10% (?). Od razu trzeba sobie powiedzieć, że ma to minimalny wpływ na percepcję, ale ciężko nie zadać sobie pytania „dlaczego?!” Wykres kończy się na 70%, natomiast czarna pozioma linia sugeruje, jakby to była maksymalna liczba punktów (szczególnie że nie widać, że są to procenty). Cztery pierwsze kategorie stanowią pewną referencję (jak wynik w podanych szkołach ma się np. do ogólnopolskich), więc warto by wyraźniej to zaznaczyć. Plus problemy estetyczne (linia przecina niektóre etykiety).
Jak zrobić to lepiej? Zaproponuję dwa rozwiązania. W pierwszym oś jest od 0 do 100%. Patrząc w ten sposób, różnice między szkołami są raczej niewielkie.
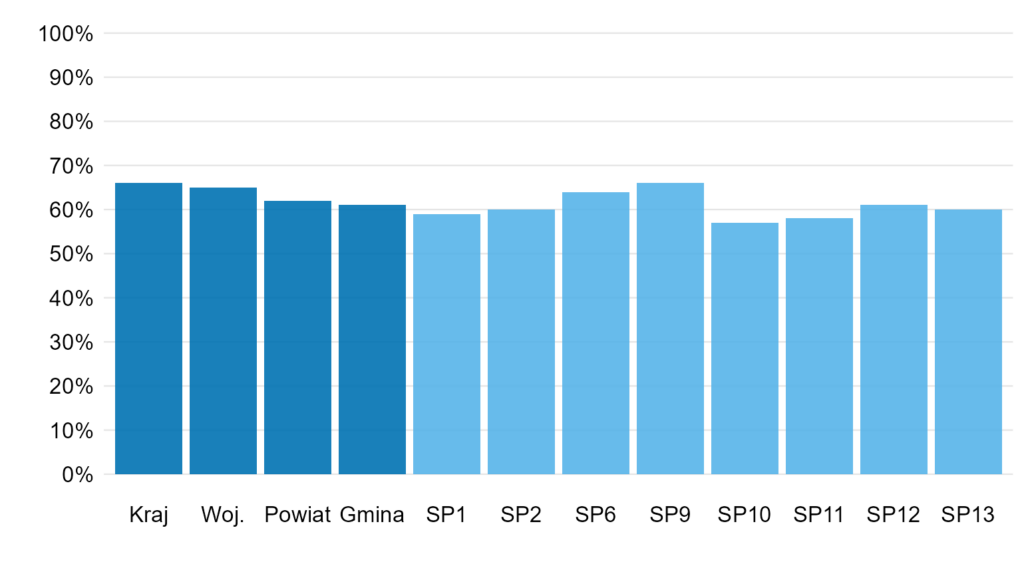
Natomiast niekoniecznie jest to najlepsze podejście. Różnica między najlepszą i najgorszą szkołą to 9 p.p. i możemy uznać, że jest to znaczące (to nie znaczy, że ma to być czysto subiektywna decyzja, ale może wynikać z głębszej analizy wyników dla całej Polski). Dlatego poniżej zrezygnowałem z osi Y aż do 100% i wyraźnie podałem wyniki nad słupkami (wtedy sama oś jest zbędna). Dodatkowo posortowałem wyniki dla szkół, ale nie twierdzę, że tak jest najlepiej. Szkoły mają swoją numery, więc jest tu pewna „naturalna” kolejność i może być warto trzymać się jej – szczególnie jeśli jest to jeden z wielu wykresów dla tych szkół.
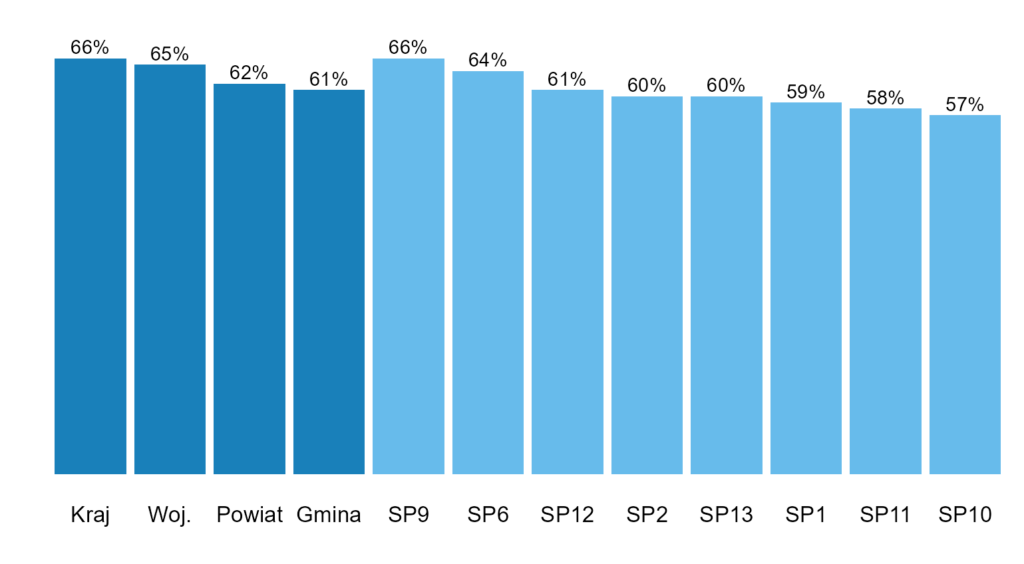
W obu przypadkach kategorie referencyjne zaznaczyłem innym kolorem, ale być może warto jeszcze wyraźniej to rozdzielić.
Wykres 9
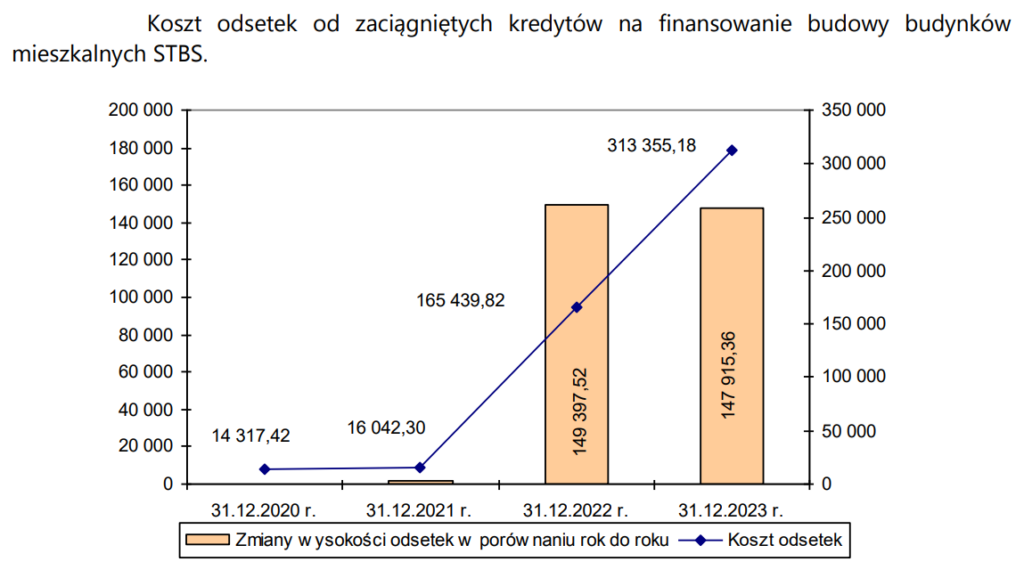
Główny problem z tym wykresem jest taki, że wydaje się bardzo skomplikowany, a tak naprawdę mamy tu tylko cztery liczby. Przy pomocy linii i punktów zaznaczono koszt odsetek, a słupki pokazują różnicę między kolejnymi punktami. Słupki są tak wysokie, bo zastosowano dwie osie Y (których niestety nie podpisano). To jest problem sam w sobie (bardzo dobre omówienie tutaj: https://flourish.studio/blog/dual-axis-charts/), ale mimo że czasem może mieć to sens, tutaj trudno to obronić, bo skale są podobne (gdyby zastosowano jedną oś, słupki wciąż byłyby dobrze widoczne).
Ogólnie ciężko powiedzieć, o co tutaj chodziło. Wyobrażam sobie, że w jakimś konkretnym przypadku w pierwszej kolejności ważne mogą być różnice w koszcie odsetek rok do roku, ale w drugiej kolejności chcielibyśmy zobaczyć, ile one dokładnie wynoszą (co do grosza…). Jeśli byłby to wykres w wewnętrznym raporcie technicznym (dla analityków, którzy są do niego przyzwyczajeni), dałoby się to obronić. Ale jego cel miał być prezentacyjny.
Poniżej moja propozycja modyfikacji. Wydaje się, że wystarczy przedstawić koszt odsetek, bo przecież różnice też są widoczne – ale zaznaczyłem je przy pomocy strzałek. Różnica między pierwszym a drugim słupkiem jest na tyle mała, że trudno ją pokazać, ale w oryginalnym wykresie również jej nie podano.
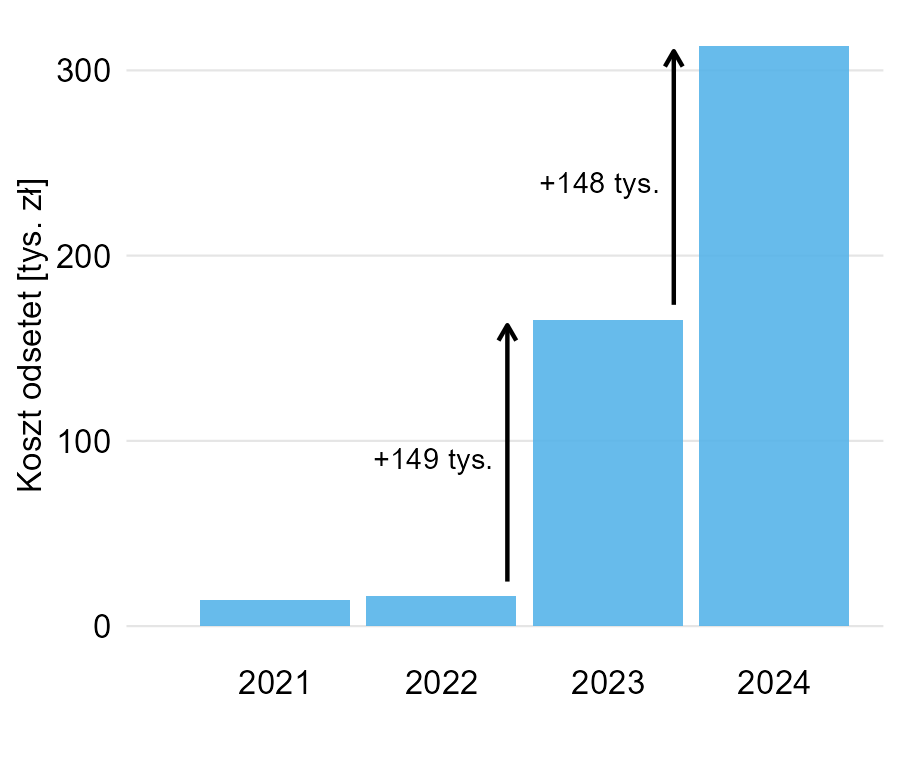
Przy okazji warto powiedzieć, że jeśli te wszystkie liczby, które pojawiają się na wykresie, są ważne, to istnieje znacznie prostsze rozwiązanie, żeby je zaprezentować: tabela. I zdaje się, że w tym przypadku byłaby znacznie bardziej przystępna niż wykres.
Wykres 10

Wykres w takiej formie wydaje się całkowicie bezużyteczny. Ciężko też powiedzieć, co było tutaj celem, w każdym razie jedyne, co widać, to jak zmieniała się liczba ogłoszeń w roku 2022 (żółte słupki) oraz jaka jest suma ogłoszeń z lat 2022-24 dla każdego miesiąca (?). Także widać tutaj okresowość (związek z miesiącem), ale ciężko przypuszczać, żeby o to chodziło (tzn. takie rzeczy też są interesujące, ale bada się je inaczej). Dodatkowo mamy mylący czarny słupek, który sugeruje, że jest jakaś całkowita możliwa liczba ogłoszeń.
Poniżej dwie moje propozycje modyfikacji. W pierwszej zachowałem zależność z miesiącem i każdy rok zaznaczyłem osobną linią. Wyraźniej zaznaczyłem najnowsze dane (rok 2024).
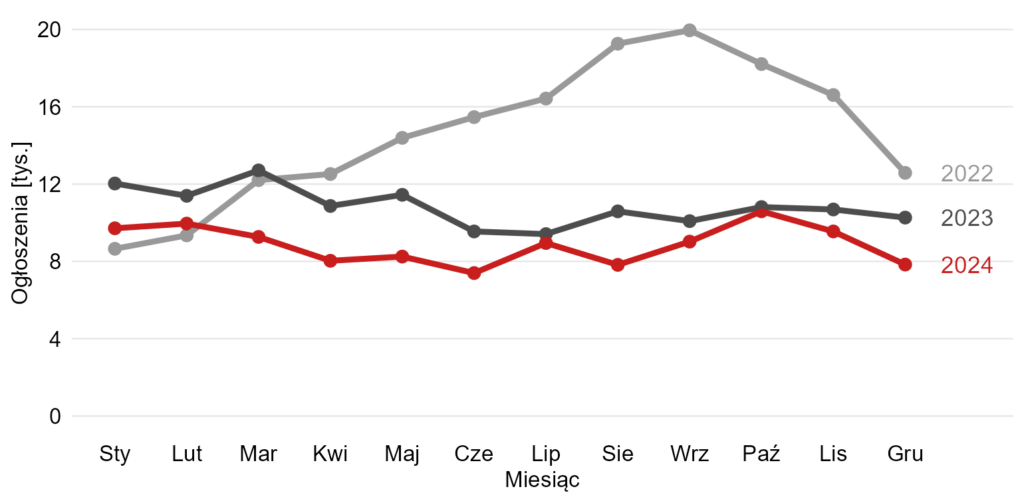
Natomiast wydaje się, że najważniejsze wnioski, które można wyciągnąć z tych danych, to po prostu jak zmieniała się liczba ogłoszeń z czasem. Dlatego poniżej najprostsze rozwiązanie.
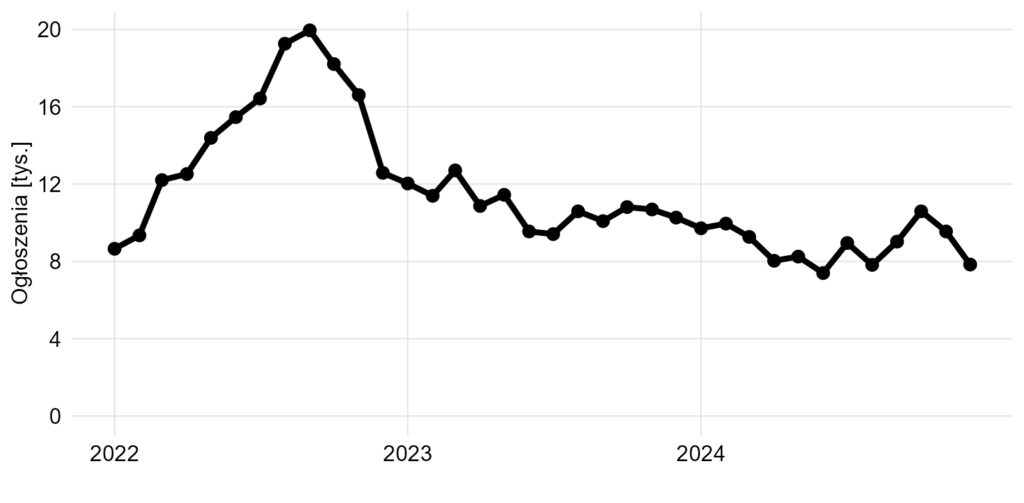
Wykres 11
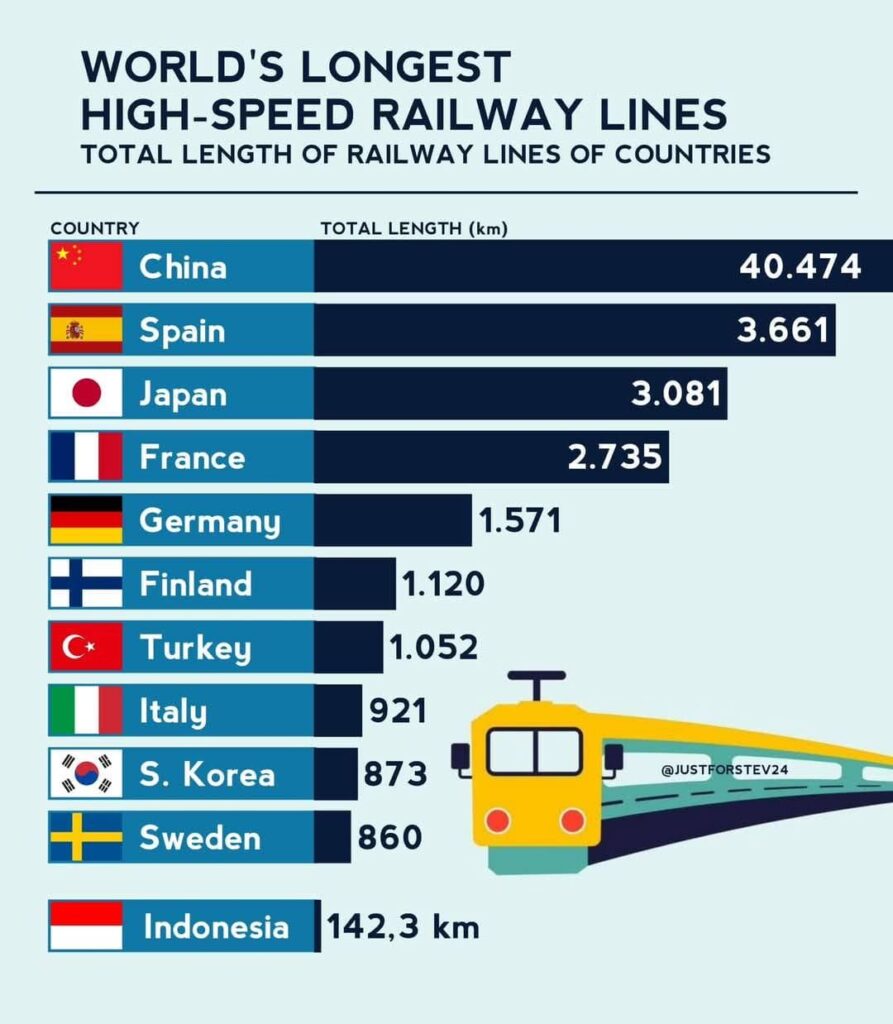
Długość linii kolejowych w Chinach jest największa, choć w Hiszpanii jest ich niewiele mniej, mimo że kraj ma znacznie mniejszą powierzchnię! A nie, czekaj…
Gdyby nie absurdalność tego wniosku, można by zastanawiać się, czy ktoś nie pomylił się o rząd wielkości w przypadku Chin, bo wtedy mniej więcej by się zgadzało. Nie ma tu nawet żadnego ostrzeżenie, że pierwszy słupek nie jest proporcjonalny do danych. Oprócz tego (choć to już szczegół) nie jest od razu jasne, czy właściwe słupki to tylko te granatowe, czy zaczynają się wcześniej (tzn. jasnoniebieskie są ich częścią).
Poniżej właściwe proporcje.

Podobnie jak w przypadku wykresu 3, można tutaj osobno zaprezentować dane dla Chin, np. sumując kilometry dla innych krajów, a na kolejnym wykresie pominąć Chiny. Czasem też zaznacza się wyraźnie, że któryś słupek nie jest pokazany w całości. Nie przepadam za tym rozwiązaniem, ale z pewnością jest to lepsze od tego, co zrobiono tutaj.
Wykres 12

Kolejny przykład, w którym oś Y służy jedynie celom propagandowym. Mamy tu jednak znacznie więcej interesujących zabiegów:
- Kolor czerwony wydaje się być bliżej niż niebieski (https://en.wikipedia.org/wiki/Chromostereopsis).
- Nieprzypadkowo wybrane zdjęcia polityków.
- Odpowiednia „interpretacja” różnic poparcia („crushes”, „destroys”).
Myślę, że jest jasne, jak to poprawić. Oczywiście przy założeniu, że chcemy przedstawić dane rzetelnie.
Wykres 13
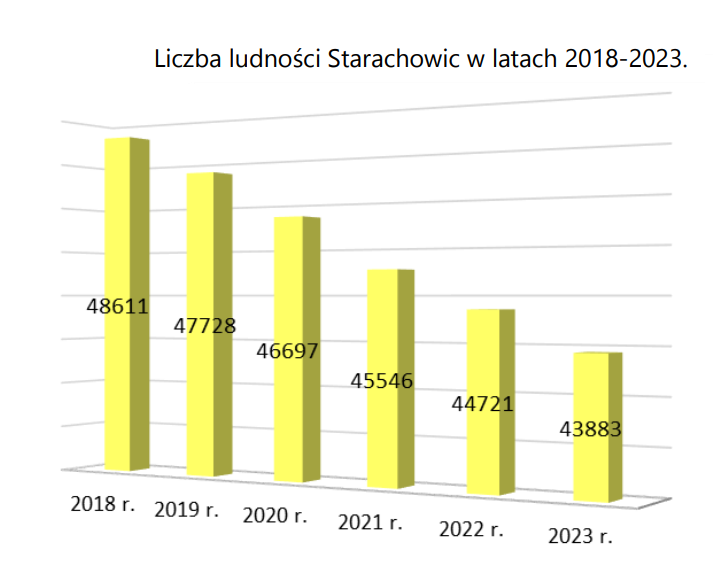
Mamy tu zupełnie niepotrzebny efekt 3D oraz patrzymy na wykres pod dziwnym kątem, choć oczywiście główny problem to tajemniczy początek osi Y. Poniżej wersja z początkiem w zerze.
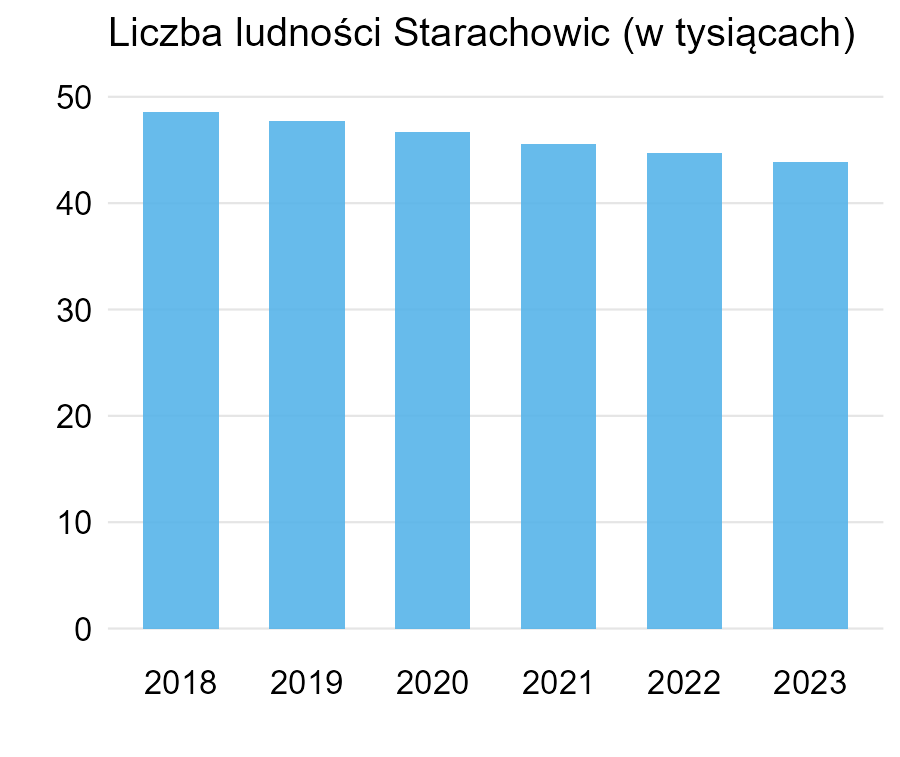
Dodajmy, że ten spadek rzeczywiście można uznać za alarmujący i pokazanie tego na wykresie nie jest proste. To jednak nie usprawiedliwia użycia wykresu słupkowego, który z zasady powinien zaczynać się w zerze. Można albo z niego zrezygnować, albo odpowiednio skomentować liczby, tak żeby czytelnik wiedział, że to nie jest mały spadek.
Wykres 14
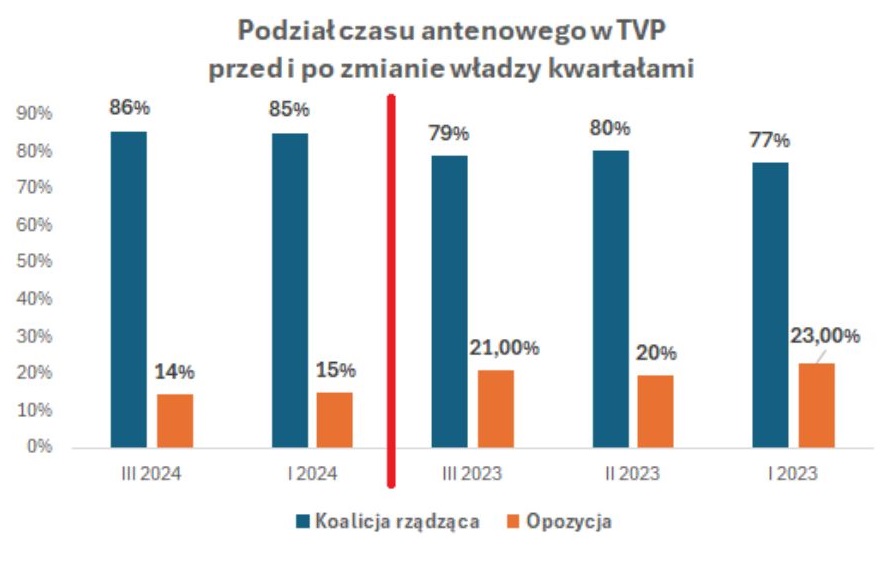
Czas na tym wykresie biegnie w lewą stronę, co łatwo przeoczyć. Brakuje niektórych kwartałów i niestety nie zostaliśmy przed tym odpowiednio ostrzeżeni. Jest tu też pewien problem z kategoriami „opozycja” i „koalicja rządząca”, gdyż należą do nich inne partie po lewej i po prawej stronie wykresu. Oczywiście można było tak do tego podejść, ale popatrzmy na poniższy wykres.
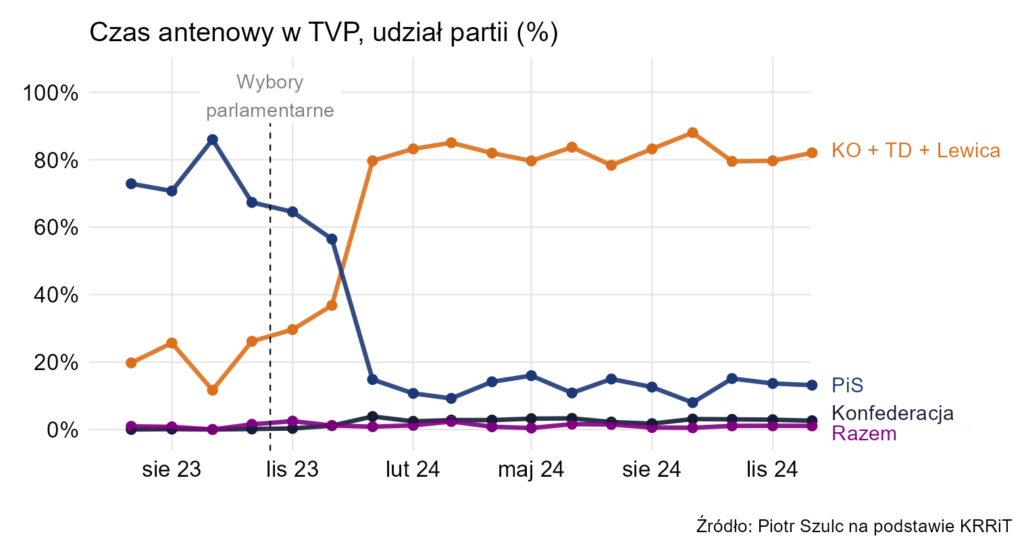
Wydaje mi się, że to, co zapewne autorzy chcieli zaprezentować na tamtym wykresie, jest teraz znacznie lepiej widoczne. Uwzględniłem też dane miesięczne, bo są dostępne.
Wykres 15
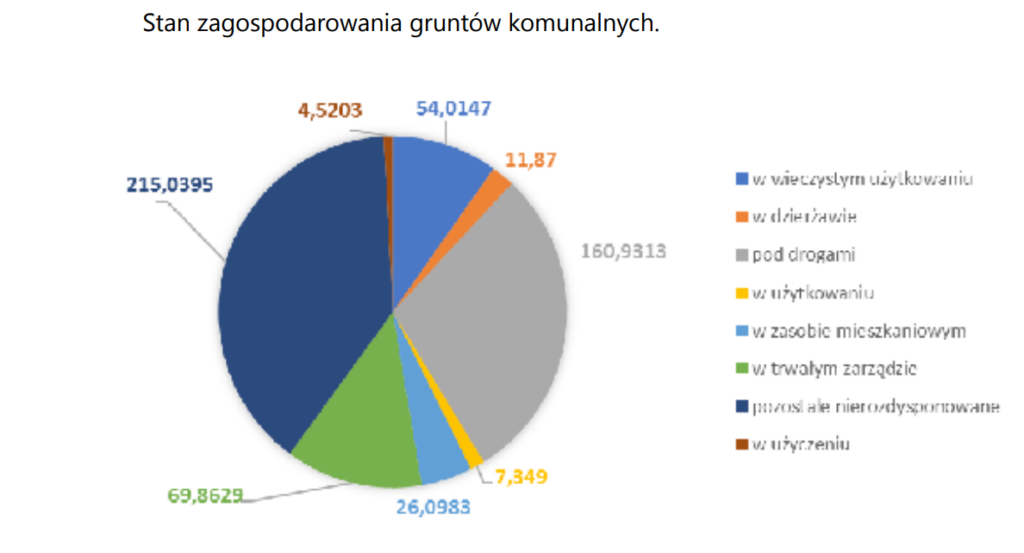
Zacznijmy od tego, że mamy tu przedstawione powierzchnie (w hektarach – niestety trzeba się tego domyślić, szczególnie że na wykresie kołowym podaje się zwykle procenty), przez co użycie wykresu kołowego dałoby się obronić. Ciężko jednak usprawiedliwić to wykonanie. Zacznijmy od tego, że odczytanie etykiet to nie lada sztuka – a w takiej formie wykres pojawił się w raporcie. Dobór kolorów i kolejność kategorii wydają się zupełnie losowe. Liczby podane z dokładnością do czterech miejsc po przecinku (to oczywiście szczegół).
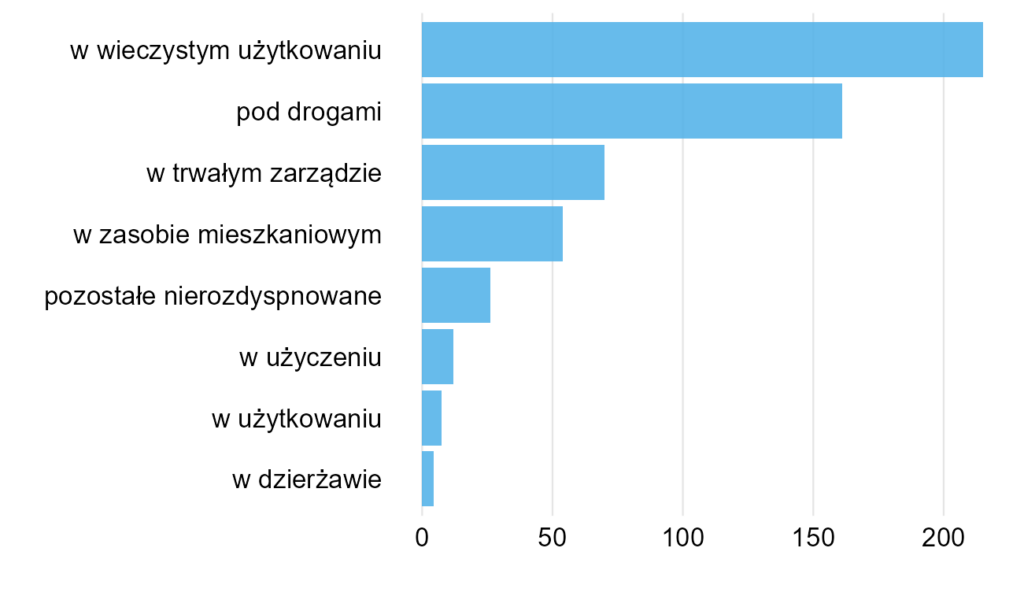
Poniżej te same dane na wykresie słupkowym.
Wykres 16
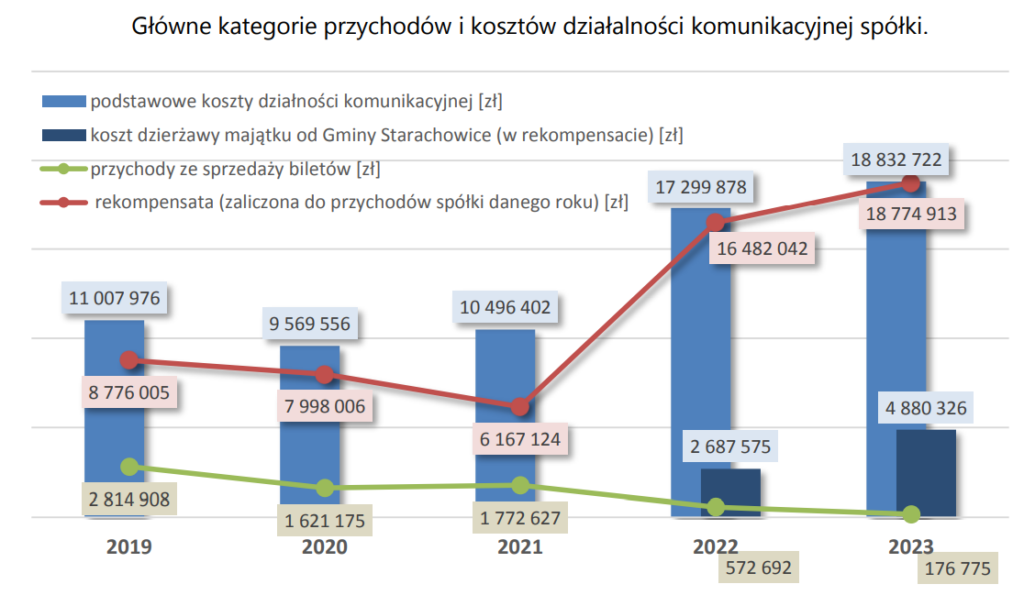
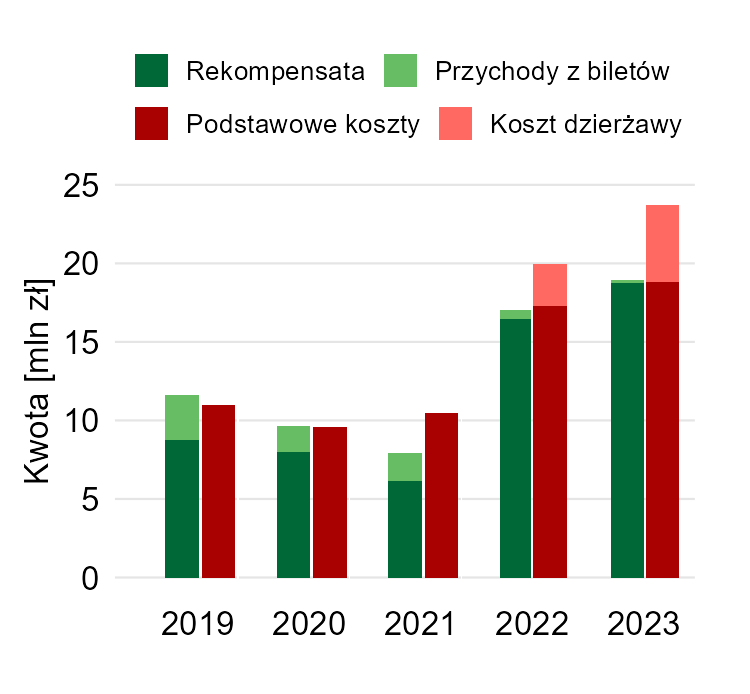
Dużo czasu trzeba spędzić, żeby odczytać ten wykres. Mamy tutaj przychody i koszty, podzielone na dwie kategorie. Przychody pokazane przy pomocy wykresu liniowego, koszty słupkowego. Takie mieszanie rodzajów wykresów rzadko kiedy jest dobrym pomysłem. Można było albo zrobić dwa osobne, ewentualnie poniżej moja wersja (być może warto było jeszcze wyraźnie zaznaczyć różnicę między przechodami a kosztami).