Wierzysz głęboko, że:
1) istnieją tylko liczby całkowite (1, 2, 3…) lub takie, które powstają poprzez ich dzielenie (1/2, 2/3, 3/2, …);
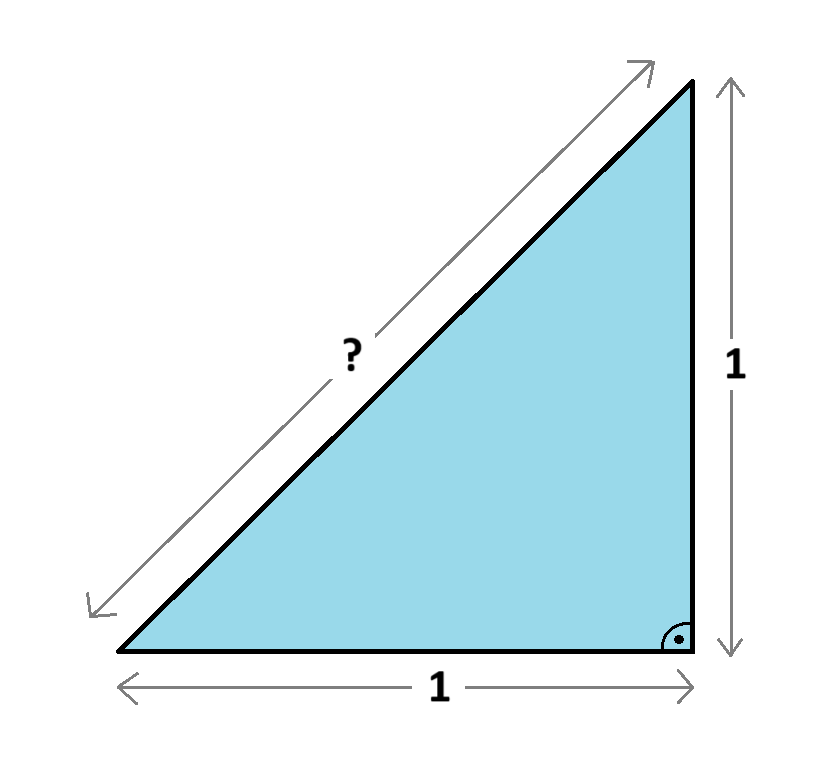
2) a^2 + b^2 = c^2, gdzie „a” i „b” to długości boków prostokąta, a „c” to jego przekątna.
Z twojej wiary (2) wynika, że jeśli weźmiemy kwadrat o boku długości 1, to druga potęga jego przekątnej wynosi 2. Ile zatem wynosi długość samej przekątnej?
Próbujesz wyrazić ją przy pomocy stosunku liczb całkowitych, bo przecież inne liczby nie istnieją. Niestety, choćbyś nie wiem, jak się starał, nie udaje ci się. Ale z (1) wynika, że po prostu za słabo się starałeś.
Pewnego deszczowego dnia przychodzi do ciebie Hippazos i dowodzi, że nigdy ci się nie uda. Twój własny uczeń! Co teraz? Przecież przekątna kwadratu ma jakąś długość, czyli musi istnieć liczba, która ją wyraża. Oba twierdzenia (1, 2) nie mogą istnieć w jednym świecie. Co robisz?
Oczywiście: topisz Hippazosa! Całe szczęście, że istnieją proste (ludzkie) sposoby na bezwzględną brutalność matematyki.
PS. Według innej legendy Hippazos został tylko wygnany. I nie tyle za sam dowód (pitagorejczycy go uznawali), ale za ujawnienie go innym ludziom (fakt, że nie wszystkie liczby da się wyrazić jako stosunek liczb całkowitych, miał pozostać tajemnicą).
PS2. Pierwiastek z dwóch, czyli bohater tej historii, jest oczywiście liczbą niewymierną – tzn. taką, której nie da się wyrazić jako stosunek liczb całkowitych. Później okazało się, że liczb niewymiernych jest więcej niż wymiernych.