Na poniższym wykresie wyniki matury z polskiego (rok 2010). To oczywiście znana sprawa i pewnie sporo osób ten wykres widziało. Jeśli nie, to pięknie pokazuje on, jak naciągano wyniki, by więcej osób zaliczyło (trzeba było otrzymać co najmniej 30% punktów, w tym przypadku 21).
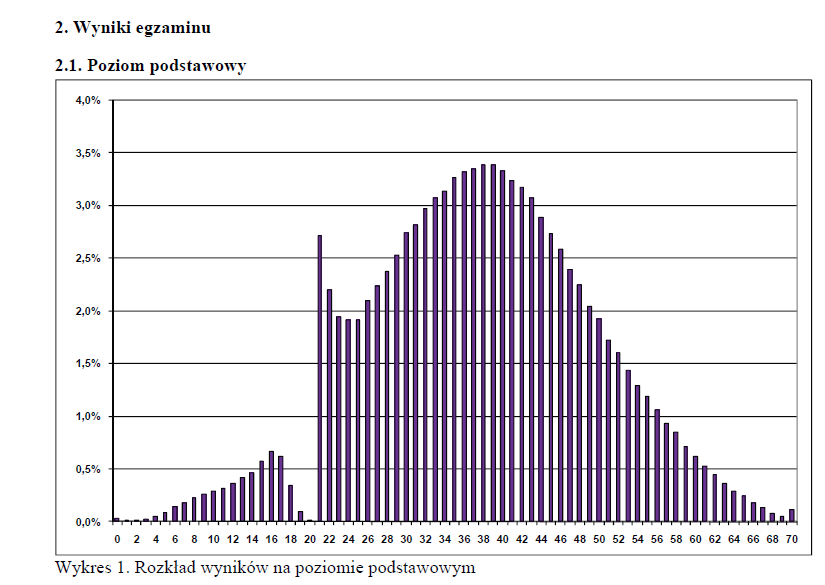
Ale jak udowodnić, że coś tu jest nie tak? Czemu rozkład wyników nie miał właśnie tak wyglądać, „naturalnie”?
Dowody?
Zacznijmy od tego, że trzeba tu dobrze rozumieć słowo dowód. Mimo że statystyka wykorzystuje aparat matematyczny, to nie można mówić o dowodzie w sensie matematycznym (proof). Udowodnić w tym przypadku oznacza: przedstawić takie argumenty, że pewna hipoteza (to jest „naturalny” rozkład wyników matur) jest nieprawdopodobna, a dalsza wiara w nią nierozsądna.
Mamy pewne wyobrażenie co do kształtu tego rozkładu — i mamy je zanim jeszcze spojrzymy na dane. Wbrew temu, co może niektórym się narzuca, wcale nie chodzi o kształt normalny (tak naprawdę ograniczenie dolne i górne, w tym przypadku 0 i 70 punktów, „przeszkadza” normalności; swoją drogą, rozkład dla matur z fizyki jest skośny). Ważniejsza jest tutaj pewna gładkość rozkładu. Pewien procent osób otrzymał 20 punktów i oczekujemy, że podobny procent otrzyma 19 i 21.
Oprócz tego, a co równie ważne, mamy bardzo dobre (prawdopodobne) wyjaśnienie, skąd taka odchyłka od tego wyobrażonego wcześniej kształtu. Biorąc obie te rzeczy pod uwagę, rozsądnie wierzyć w hipotezę o naciąganiu.
Nowa wiedza i jej ograniczenia
Zobaczmy, że w wyniku takiego prostego podsumowania danych pozyskaliśmy nową wiedzę. Ciężko byłoby dojść do niej, analizując każdy z wyników osobno, i to mimo że efekt jest tak wyraźny. Co więcej, da się ten efekt przedstawić ilościowo, choć tu już nie wystarczy sama gładkość rozkładu, ale trzeba założyć pewne tempo wzrostu wysokości słupków (np. rozkład normalny). Patrząc na wykres, szacuję, że ok. 2,5% osób ma naciągnięty wynik (suma brakujących długości słupków). Widać też, że naciągano już od 17 punktów oraz czasem bardziej, niż trzeba (słupki dla 22 i 23 punktów też są za wysokie).
Dobrze, a kto miał zawyżony wynik?
I to jest ciekawe, że nie wiadomo. Zdobyliśmy pewną wiedzę, patrząc z daleka, ale też odnosi się ona do odpowiedniego dystansu (jest ogólna). I to mimo że tak precyzyjnie udało nam się pewne rzeczy podać.
Jeśli weźmiemy pracę, która otrzymała 21 punktów, z pewnym prawdopodobieństwem (które też można oszacować!) jest to naciągane, z pewnym nie (bo przecież niektórzy rzeczywiście napisali na 21 punktów). Żeby kogoś złapać za rękę, musimy sprawdzić jeszcze raz wszystkie prace od 21 do 23 punktów (a może nawet 24).
Wybory w Rosji
Sprawdźmy teraz wyniki wyborów w Rosji. To, że dobrotliwy egzaminator dodał komuś parę punktów do wyników matury, to przecież nic takiego. Wybory to poważniejsza sprawa.
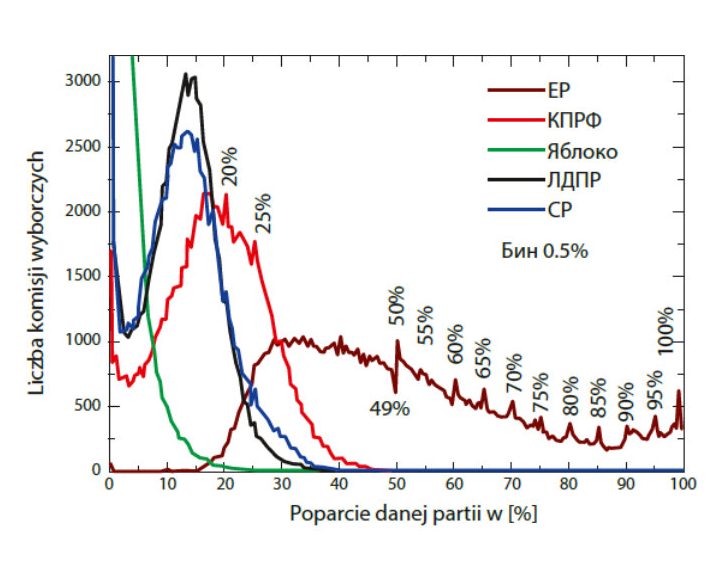
Najpierw trzeba dobrze zrozumieć, co powyższy wykres przedstawia. Weźmy partię X. W jednej komisji wyborczej zagłosowało na nią 30% osób, w innej 40% itd. Interesuje nas, w ilu z nich partia X otrzymała np. dokładnie 40% (plus/minus 0,5%). Na osi Y mamy właśnie liczbę komisji wyborczych, w których głos na daną partię oddał pewien konkretny procent głosujących.
Tak, jest to dość specyficzne przedstawienie wyników wyborów. Natomiast podobnie jak z maturami, tu również należy oczekiwać pewnej gładkości. Jeśli partia otrzymała 42% w 1000 komisji, to w podobnej liczbie komisji powinna otrzymać 41% i 43%. Z jakiegoś tajemniczego powodu jest jednak inaczej. „Okrągłe” liczby (wielokrotności 5%) pojawiają się częściej. Bardzo charakterystyczne jest też maksimum lokalne dla 50% i minimum dla 49%.
Nie jest łatwo oszukiwać…
Jak to wyjaśnić? Zamiast liczyć, ile dana partia otrzymała głosów, najpewniej podawano ją z głowy (czy też na podstawie wytycznych…), a człowiek ma dużą trudność, żeby zrobić to dobrze, tzn. żeby nie wyszło potem, że pewne liczby pojawiają się zbyt często. Nie potrafimy losować z rozkładu jednostajnego (ani z żadnego innego). Najwyraźniej preferowano „ładne” liczby — może dlatego, żeby łatwiej było zadbać o to, by sumowały się do 100% (zwróćmy uwagę na piki w 20 i 25% dla partii, która nie wygrała).
Patrząc na ten wykres, warto też docenić, że analityk, który go stworzył, najpewniej musiał wykonać sporo roboty. Nie jest to standardowe spojrzenie na tego typu dane i najpewniej wykonanych zostało wiele innych wykresów, które nie ujawniły oszustwa. Ale w końcu to wylezie. Powiedzcie komuś, żeby w myślach rzucił dwiema kostkami i podał wyniki. Nie udowodnicie, że naprawdę nimi nie rzucał. Ale zbierzcie 1000 takich wyników i policzcie, jak często na obu kostkach „wypadło” to samo. Czy mniej więcej 1/6 razy? Wątpię.
Oj, trudno jest udawać losowość, a przez to trudno oszukiwać. Zawsze znajdzie się jakiś wredny statystyk i to wykryje. Nawet jak zadbasz o jeden aspekt, najpewniej nie uwzględnisz innego. Słyszeliście o rozkładzie Benforda?
Wybory w Polsce
Spójrzmy na załączoną mapkę. Kolorem przedstawiono procent nieważnych głosów w wyborach samorządowych (2010), w wyniku postawienia co najmniej dwóch krzyżyków (czyli to nie są wszystkie nieważne głosy).
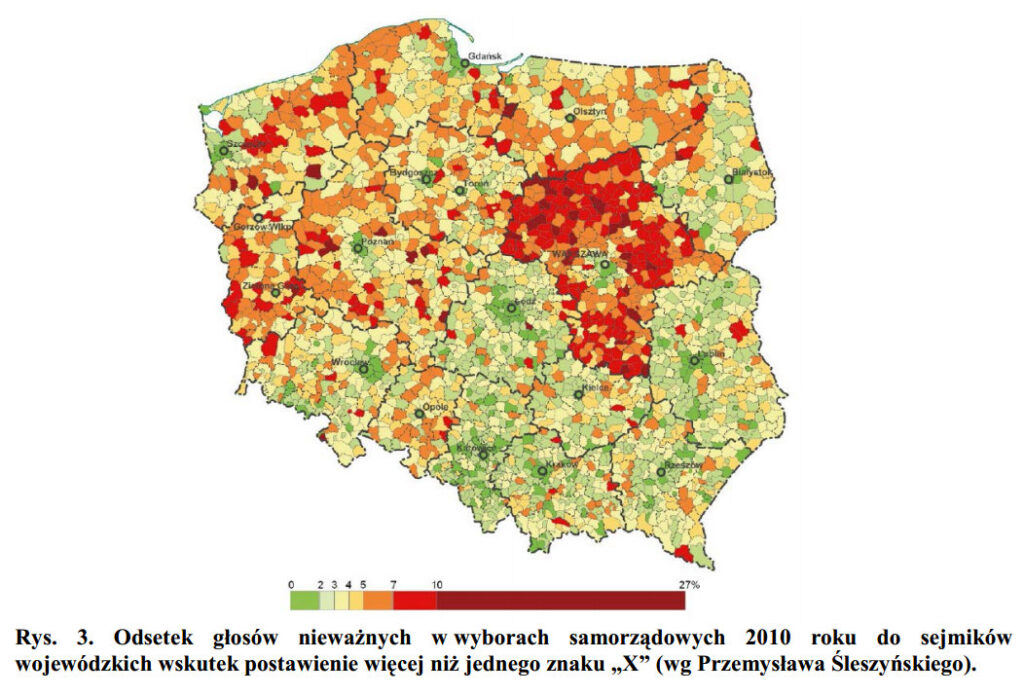
Jak widać, wyższy procent wyraźnie pokrywa się z granicami województwa mazowieckiego. W graniczących powiatach potrafią zagłosować, ale tam, za miedzą, to głupie ludzie mieszkają i nie rozumieją.
Ponieważ ta hipoteza jest nieprawdopodobna, stawiamy inną. Pamiętacie powszechnie zdziwienie, że PSL zdobył tyle głosów, mimo że w sondażach był pod progiem? Tak się składa, że był wtedy pierwszy na liście. W województwie mazowieckim nie było jednej karty go głosowania, ale „książeczka”. Po zakończonym głosowaniu wszystkie wędrują w jedno miejsce. Tam jakiś sympatyk PSL dostawia krzyżyki. Nie musi nawet otwierać karty. Jest krzyżyk na pierwszej stronie? Świetnie, bierzemy kolejną kartę. Nie ma iksa? Szkoda — dostawiamy. Oczywiście taki głos będzie nieważny, ale tym samym zwiększamy liczbę głosów nieważnych na nie-PSL, czyli zwiększamy proporcję głosów na PSL.
Przekonałem Was?
Narracja
Łatwo ulec tego typu narracji, szczególnie jeśli jest poparta dobrą wizualizacją. Zwykle jednak rozsądniej poszukać innych, prostszych wyjaśnień. Oszustwo to poważna sprawa i wymaga bardzo dużo nakładów. Prostsze wyjaśnienie jest bardziej prawdopodobne (a priori!), bo wymaga ich mniej. Łatwo też popełnić błąd jednej przyczyny. Rzadko kiedy jakieś zjawisko da się wyjaśnić innym pojedynczym zjawiskiem.
W przypadku tych nieważnych głosów, istnieje proste i logiczne wyjaśnienie (sam nie wiem, ile z tego wyżej nazmyślałem; chyba SLD było wtedy pierwsze na liście). Otóż ta książeczka była TYLKO w województwie mazowieckim. I cóż, część osób się pogubiła. Być może myślała, że na każdej stronie trzeba zaznaczyć poprawną odpowiedź…
Oczywiście to też jest problem i mogło to wpłynąć na wyniki wyborów — bo te nieważne głosy prawie na pewno nie układają się losowo.
Czyli wiecie: jak już oszukiwać, to tak, żeby istniało prostsze wyjaśnienie.
Jeśli moje teksty są dla Ciebie wartościowe, na podany niżej adres email mogę przesłać Ci wiadomość, gdy pojawią się nowe. Zapraszam też na mój kanał na youtube.



